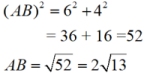|
For a review of translations, see the Refresher section Transformations: Translations.
Now let's expand that knowledge of translations in relation to geometry.
 |
A translation is a rigid transformation of the plane that moves every point of a pre-image a constant distance in a specified direction. |
|
A translation (notation Ta,b ) is a transformation which "slides" a figure a fixed distance in a given direction. In a translation, ALL of the points move the same distance in the same direction.
The points all move parallel to one another.
Tab(x,y) = (x + a, y + b)
A translation is a rigid transformation or isometry because
the image is the same size and shape as the pre-image.

|
|
In this translation that maps ΔABC to ΔA'B'C', the distances from the pre-image points to the image points are equal, and the segments representing these distances are parallel.
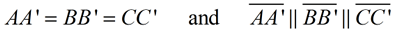
In addition, the corresponding segment sides of the pre-image and images are parallel. 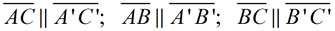
Orientation (lettering): The lettering of the points of the pre-image, in this diagram, is counterclockwise A-B-C, and the image is also lettered counterclockwise A'-B'-C'. When lettering order remains the same, the transformation is referred to as a direct isometry. |
Properties preserved under a translation from the pre-image to the image.
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
5. orientation (lettering order remains the same)
|
|
|

There are several ways to designate a translation:
mapping:
Example:
(x, y) → (x + 8, y - 6)
Read: "the x and y coordinates are mapped to x + 8 and y - 6 respectively".
|
notations:
Example: T8,-6
or
T8,-6 (x, y) = (x + 8, y - 6)
The 8 tells you to "add 8" to all x-coordinates, while the -6 tells you to "subtract 6" from all of the y-coordinates.
|
description:
Example:
"8 units to the right and 6 units down."
A verbal or written description of the translation is given. |
| Movement: Remember that adding a negative value (subtracting), indicates movement left and/or down, while adding a positive value indicates movement right and/or up. |
Using vectors to show movement of a translation:
A translation displaces every point in the plane by the same distance, in the same direction, and can be described using a vector.
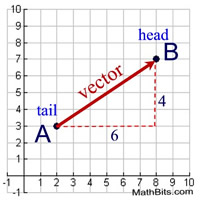
A vector is represented by a "directed line segment", a segment with an arrow at one end indicating the direction of movement. Unlike a ray, a "directed line segment" has a specific length. The Pythagorean Theorem can be used to find the length of a vector in the coordinate plane.
Vectors used in translations are what are known as "free vectors", which are a set of parallel "directed line segments". A vector translation moving "8 units to the right and 6 units down" can be written as 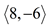 . You may also see  . . |
|


Translations in the Coordinate Plane:
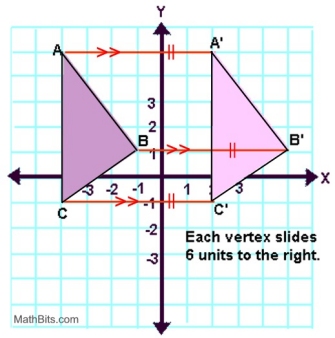 |
Horizontal Translation
Horizontal movement only:
(x, y) → (x + 6, y)
The x-values are moving,
but the y-values stay the same.
Notice that the three red line segments indicating movement are of equal length, and are parallel.
In the expression x + 6, the plus sign indicates the positive "direction" of the movement (to the right on the grid),
(a negative sign indicates movement to the left) |
|
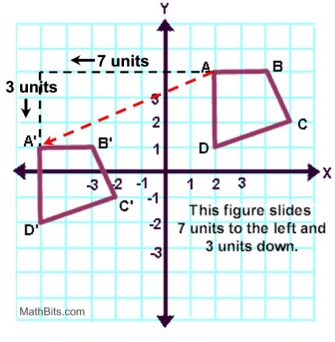
Diagonal Translation
It is possible to combine the idea of vertical and horizontal translations to create diagonal translations.
(x, y) → (x - 7, y - 3)
Notice the formation of a right triangle indicating the horizontal and vertical components of the translation. The actual transformation movement becomes the hypotenuse of the right triangle.
The Pythagorean Theorem can be used to find the "distance" from A to A'.
|
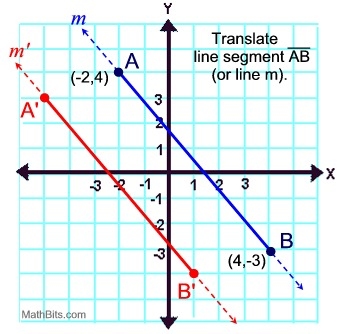 |
Translating Segments (or Lines)
Consider the translation
(x, y) → (x -3, y - 1)
as applied to the segment (line)
shown at the left.
Since a translation is a "slide", the slopes of segments (or lines) do not change.
Thus, the translation of a segment (or line) produces another segment (or line) with the same slope, making the segments (or lines) parallel.
* Notice how the corresponding segment sides of the figures in the previous examples also remain parallel to one another. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|